In this work, a combined modelling approach for crack propagation in defective graphene is presented. Molecular dynamics (MD) simulations are used to obtain material parameters (Young's modulus and Poisson ratio) and to determine the energy contributions during the crack evolution. The elastic properties are then applied in phase-field continuum simulations which are based on the Griffith energy criterion for fracture. In particular, the influence of point defects on elastic properties and the fracture toughness are investigated. For the latter, we obtain values consistent with recent experimental findings. Further, we discuss alternative definitions of an effective fracture toughness, which accounts for the conditions of crack propagation and establishes a link between dynamic, discrete and continuous, quasi-static fracture processes on MD level and continuum level, respectively. It is demonstrated that the combination of MD and phase-field simulations is a well-founded approach to identify defect-dependent material parameters.
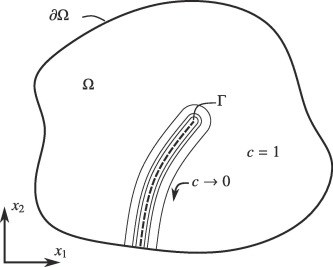
In this work, a combined modelling approach for crack propagation in defective graphene is presented. Molecular dynamics (MD) simulations are used to obtain material parameters (Young's modulus and Poisson ratio) and to determine the energy contributions during the crack evolution. The elastic properties are then applied in phase-field continuum simulations which are based on the Griffith energy criterion for fracture. In particular, the influence of point defects on elastic properties and the fracture toughness are investigated. For the latter, we obtain values consistent with recent experimental findings. Further, we discuss alternative definitions of an effective fracture toughness, which accounts for the conditions of crack propagation and establishes a link between dynamic, discrete and continuous, quasi-static fracture processes on MD level and continuum level, respectively. It is demonstrated that the combination of MD and phase-field simulations is a well-founded approach to identify defect-dependent material parameters.
