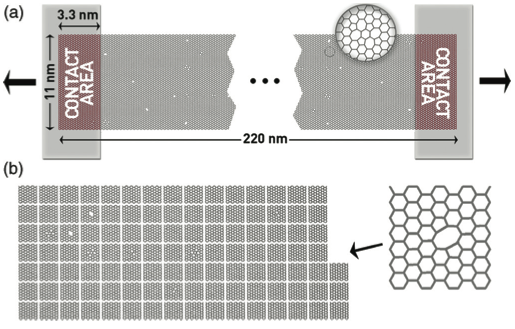
We investigate the combined influence of structural defects and uniaxial longitudinal strain on the electronic transport properties of armchair graphene nanoribbons using the numerical approach based on the semiempirical tight-binding model, the Landauer formalism, and the recursion method for Green functions. We calculate the conductance of graphene nanoribbons in the quantum coherent regime with different types and concentrations of defects. Further, we apply uniform planar tension to the nonideal graphene ribbons with randomly distributed and oriented single and double vacancies and Stone-Wales defects. Since transport characteristics of graphene nanoribbons are found to be very sensitive to edge termination and aspect ratio, and it has been shown that energy gaps can emerge under critical strain; the interplay of both effects needs to be studied. We show that band gap engineering using strain is still possible for nonideal armchair ribbons with a small defect concentration, as the oscillatory behavior of the gap is preserved.