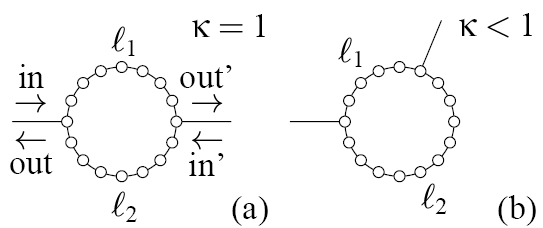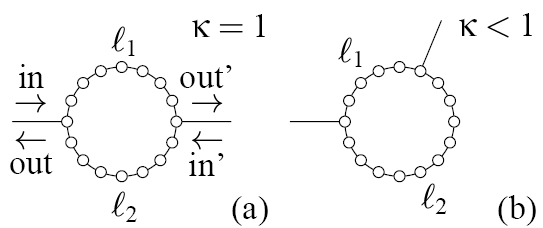
We examine the anomalous behavior of the transmittance through a one-dimensional ring having two branches of different lengths, as determined by the lead positions. Jumps in the transmittance phase are occurring in correspondence to both (a) zeros in the transmission at the eigenstates of the isolated ring and (b) destructive interference events. It is also found that when the ratio of the branch lengths is given by p/qsatisfying p+q = 0mod{4}, the two characteristic zeros merge into a single point and the transmittance phase becomes identical to the so-called Friedel phase.