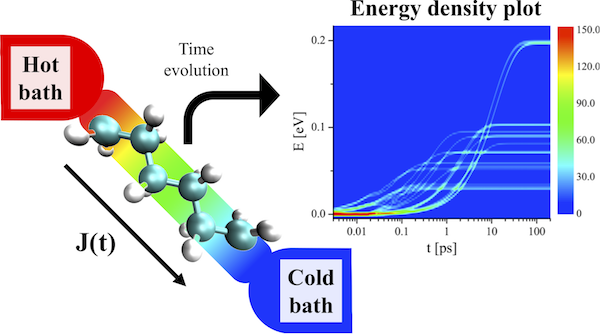
Phonons play a major role for the performance of nanoscale devices and consequently a detailed understanding of phonon dynamics is required. Using an auxiliary-mode approach, which has successfully been applied for the case of electrons, we develop a new method to numerically describe time-dependent phonon transport. This method allows one to gain insight into the behavior of local vibrations in molecular junctions, which are driven by time-dependent temperature differences between thermal baths. Exemplarily, we apply the method to study the nonequilibrium dynamics of quantum heat transport in an one-dimensional atomic chain as well as in realistic molecular junctions made of polyacetylene and polyethylene chains, in which the vibrational structure of the junction is described at the density functional theory level. We calculate the transient energies and heat currents and compare the latter to the standard Landauer approach in thermal equilibrium. We show that the auxiliary-mode representation is a powerful and versatile tool to study time-dependent thermal transport in nanoscale systems.