The chirality-induced spin selectivity effect has been confirmed experimentally for a large class of organic molecules. Adequately modeling the effect remains a challenging task, with both phenomenological models and first-principles simulations yielding inconclusive results. Building upon a previously presented model by K. Michaeli and R. Naaman [J. Phys. Chem. C 123, 17043 (2019)], we systematically investigate an effective 1-dimensional model derived as the limit of a 3-dimensional quantum system with strong confinement and including spin-orbit coupling. Having a simple analytic structure, such models can be considered a minimal setup for the description of spin-dependent effects. We use adiabatic perturbation theory to provide a mathematically sound approximation procedure applicable to a large class of spin-dependent continuum models. We take advantage of the simplicity of the models by analyzing its structure to gain a better understanding how the occurrence and magnitude of spin polarization effects relate to the model's parameters and geometry. The obtained spin polarization is not strongly dependent on the strength of the spin-orbit interaction, but it rather results from breaking time-reversal invariance upon selection of a given angular momentum of the incoming electrons.
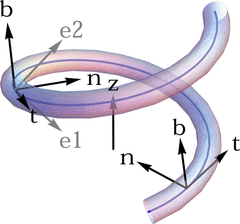
The chirality-induced spin selectivity effect has been confirmed experimentally for a large class of organic molecules. Adequately modeling the effect remains a challenging task, with both phenomenological models and first-principles simulations yielding inconclusive results. Building upon a previously presented model by K. Michaeli and R. Naaman [J. Phys. Chem. C 123, 17043 (2019)], we systematically investigate an effective 1-dimensional model derived as the limit of a 3-dimensional quantum system with strong confinement and including spin-orbit coupling. Having a simple analytic structure, such models can be considered a minimal setup for the description of spin-dependent effects. We use adiabatic perturbation theory to provide a mathematically sound approximation procedure applicable to a large class of spin-dependent continuum models. We take advantage of the simplicity of the models by analyzing its structure to gain a better understanding how the occurrence and magnitude of spin polarization effects relate to the model's parameters and geometry. The obtained spin polarization is not strongly dependent on the strength of the spin-orbit interaction, but it rather results from breaking time-reversal invariance upon selection of a given angular momentum of the incoming electrons.
